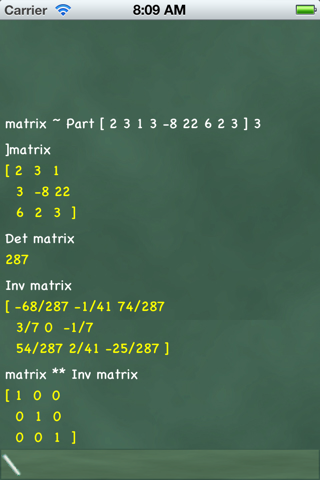
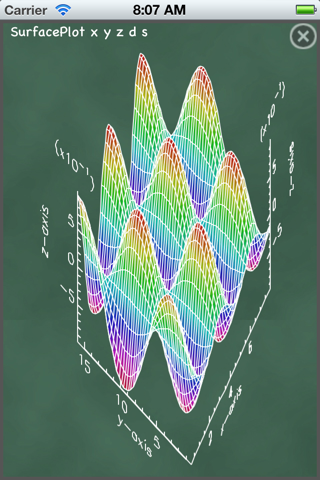
Gnomon is an interactive, programmable calculator with a standard library of mathematical, statistical and plotting functions.
The name Gnomon comes from an ancient Greek word signifying "one that knows", an interpreter, discerner. (In English the word is used to describe the shadow casting indicator of a sundial.)
Calculations can be entered directly into the interactive command table, and a history is maintained. A calculator-like easy input keyboard is available, or the standard keyboard may be used with a custom keyboard accessory that minimises the need to switch keyboards while entering mathematical symbols. Freeform text entry via worksheets is also supported, and maintained between invocations.
Large output and graphics are shown in abbreviated form but can easily be recalled. Plots can be scaled, saved, and 3D plots can be rotated.
Command entry may be anything from simple expressions to complicated user functions, loops, conditions. Data in the form of integers (arbitrary precision), fractions, decimals, complex numbers, arrays, strings, stacks and dicionaries are natively supported. Extensive help is included with the app, and the freeform worksheets are pre-populated with illustrative examples.
Scroll the main window horizontally to switch between the various modes of operation - interactive, freeform, function reference and help.
A major language enhancement introduced in version 2.1 is support for Anonymous Functions. Such functions make using any standard library functions that require a function argument much easier. The capability is described in the language definition in more detail, but as one example
a~[[10]];FnFill a @{GRand 10 5}
will create and fill the array "a" with values numbers from a Gaussian distribution with mean 10 and standard deviation 5. As another example
FLinePlot @{CCDF 0 1 ?1} [-5:5:0.1] AxesPlotDefs LineDefs
makes it possible to plot the Cauchy distribution function with parameters 0 and 1 without having to define another function that takes a single x variable.